SATOR - Устный счет

АДРЕС	SATOR.ucoz.ru
исправлено 2013.07.21
ДЕНЬ УЧИТЕЛЯ
УСТНЫЙ СЧЕТ
... Задачи воспитания и образования это задачи государственной важности Пирогов НИ (1810-1881)
1.КНИГИ 2.ФИЛЬМЫ 3.МУЗЫКА 4.СТАТЬИ 5.КАРТИНЫ 6.ПЕДАГОГИ

Богданов-Бельский НП (1868-1945)
НЖ 2005.12.65-66 Статью В. Доценко «Пятое правило арифметики» (№ 12, 2004 г.) читал с огромным интересом. Но начну свой отклик издалека, со ссылки на одну давнишнюю вашу публикацию. Был в свое время среди авторов журнала известный специалист по информатике и автоматическому управлению — А. И. Кобринский. В 1960-х годах он поместил в вашем журнале забавную юмореску, своего рода репортаж из будущего. Будто бы собирается в недрах Пентагона сверхсекретное совещание. Приглашенным объясняют: «Один парень изобрел бумажный компьютер!» То есть он заново открыл приемы счета на бумаге, к тому времени напрочь забытые. Прошло сорок лет. Предсказание Кобринского сбывается на наших глазах. Как оно сбылось во Франции, красочно рассказывает В. Доценко. Но то же явление имеет место и в Германии. Журнал «Шпигель» (№ 50, 2004 г.) поместил подборку материалов об уровне математических знаний немецких школьников, но точнее было бы сказать — об уровне незнания. Констатируется, что в ряде случаев неумение считать доходит до уровня дизлексии (это такое умственное расстройство, при котором человек, зная буквы, не может сложить из них слова, не может читать). В нашем случае речь идет о невозможности счета, поэтому авторы говорят о дизкалькулии: многие школьники не могли оценить, что больше — 34 или 43. У меня нет документальных данных о том, как обстоят дела с устным счетом в нашей школе сейчас. Зато есть живописное в буквальном смысле свидетельство того, как они обстояли век назад. Я имею в виду картину Богданова-Бельского «Устный счет» 1896). Сельская школа. Ученики в лаптях. Сосредоточились, ушли в себя. На доске задача:

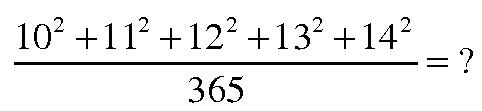Кому в наши дни посильна эта задача в качестве устного упражнения? Кстати, эта задача не только на устный счет, но и на сообразительность. Немного подумав, можно догадаться, что ответ равен двум. (Один из вариантов решения см. на стр. 132.) Могут сказать: скорее всего, внимание художника привлекла школа выше среднего уровня. Возможно. Но все равно — школа то народная. А в российской народной школе устный счет всегда занимал должное место. Но так ли уж нужно уметь считать устно в эпоху калькуляторов? Времена изменились... Мне кажется, что устный счет не просто полезный бытовой навык. Это одно из средств оценки и прогнозирования обстановки, инструмент самостоятельного мышления. Г. ПОЛОЗНЕВ (г. Бердск Новосибирской обл.). СБЫВШЕЕСЯ ПРЕДСКАЗАНИЕ (См. стр. 65.) На картине тверского художника Николая Петровича Богданова-Бельского «Устный счет», написанной в 1895 году, изображена сценка на уроке арифметики в сельской школе, который проводит Степан Александрович Рачинский. Степан Александрович был профессором Московского университета. Ему прочили блестящее будущее, но после конфликта с руководством оставил кафедру и уехал в свое имение учить грамоте сельских детей. В конце XIX века Рачинский издал несколько сборников задач для решения в уме и книг по методике преподавания арифметики. Задачу, написанную на доске, можно решать в уме разными способами. Вот один из них. Рассмотрим числитель дроби и преобразуем его в более простой вид:

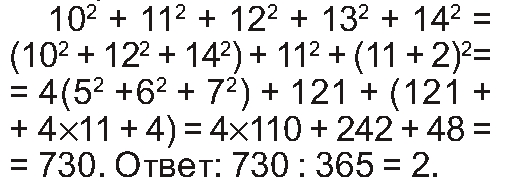Свои варианты решения вы можете прислать в редакцию. Наиболее интересные из них будут опубликованы.
ПЕРЕЛЬМАН Я.И (0000-0000) Задача в самом деле нелегкая. С нею, однако, хорошо справлялись ученики того учителя, который с сохранением портретного сходства изображен на картине, именно С. А. Рачинского, профессора естественных наук, покинувшего университетскую кафедру, что-бы сделаться рядовым учителем сельской школы. Талантливый педагог культивировал в своей устный счет, основанный на виртуозном использовании свойств чисел. Числа 10, 11, 12, 13 и 14 обладают любопытной особенностью: 102+112+122 =I32+142.. Так как 100+121 + 144 = 365, то легко рассчитать в уме, что воспроизведенное на картине выражение равно 2. Алгебра дает нам средство поставить вопрос об этой интересной особенности ряда чисел более широко: единственный ли это ряд из пяти последовательных чисел, сумма квадратов первых трех из которых равна сумме квадратов двух последних? РЕШЕНИЕ Обозначив первое из искомых чисел через х, имеем уравнение x²+ (x+1)²+ (x+2)²= (x+3)²+ (x+4)². Удобнее, однако, обозначить через х не первое, а второе из искомых чисел. Тогда уравнение будет иметь более простой вид (x—1)²+x²+(x+1)²=(x+2)²+(x+3)² Раскрыв скобки и сделав упрощения, получаем: x²-10x-11=0 откуда x = 5± &radic 5 + 11, x1 = 11, х² = -1 Существуют, следовательно, два ряда чисел, обладающих требуемым свойством: ряд Рачинского 10, 11, 12, 13, 14 и ряд —2, —1, 0, 1, 2. В самом деле, (—2)²+(—1)²+0²=1²+2²
АВТОРСКИЕ ПРАВА SATOR.ucoz.ru старается СТРОГО соблюдать Закон авторства. ВСЕ материалы имеют указание автора и / или ссылку на исходный материал. Компилятивные материалы имеют список использованных работ. При обнаружении материалов не соответствующих вышеприведенным Правилам - нижайще прошу сообщить по АДРЕСУ Материалы помещатся на SATOR.ucoz.ru БЕЗ СОГЛАСОВАНИЯ с Авторами (при всем желании это не получатся). НО при малейшем писке протеста или замечании материал снимается НЕМЕДЛЕННО и НАВСЕГДА.